Getting started on Udemy with SAP ABAP Programming for Beginners by Peter Moxon is just a matter of few steps. First of all, create your Udemy account by simply signing up.

Log in to your account and purchase the courses you wish to study. Once you have purchased, you have lifetime access to the on-demand videos. You can get a brief idea about what this course contains from here.

The course- SAP ABAP Programming for Beginners is a 13 hours video lecture lesson. There are a total of 13 modules and today we shall describe module 3.

In this module, Peter Moxon has laid emphasis on Performing Calculations of the SAP ABAP programming. The entire module is of 22 minutes. The module is split into 6 parts. The videos are short and to the point. Each part is described in the upcoming sections.

We have learned to create variables. We can move on and use these variables in calculations within our program. We’re going to have a look at some of the simple arithmetic covering addition, subtraction, division, and multiplication.

Arithmetic Addition

First of all, let’s have a look at addition. It’s very simple. So let’s say our program needs to add two numbers together. Each number is stored in its own unique variable and we want to store the product of the two numbers in a brand new variable that we can call result. So first, we’ll declare a new data variable and use the like statement.

DATA integer01 TYPE i VALUE 22

DATA packed_decimal01 TYPE p DECIMALS 1 VALUE ‘5.5’

DATA result LIKE packed_decimal01

We’ll make it the same as decimal01. It doesn’t take much in the way of the code to add two numbers together. All we need to do is write the result, which is a variable that we declare.

Copy integer01 + packed_decimal01 with a full stop at the end. Click Pretty printer and check it. The syntax should be correct. So let’s take a look at what this program actually does. It’s just adding integer01 and packed_decimal01 and putting the product of those two into the variable results.

To check, add the written statement and we’ll just write the results. Activate the program. We can see the result is 16.5. Let’s go through this a little bit deeper.

Result = integer01 + packed_decimal01

Write/result

Even though it looks super simple there are a few things that we need to consider carefully. The first one is that for any arithmetic operations, we always have to have the equal sign to the left of the actual calculation, and the variable to hold the result is to be the left of the equal sign.

The calculation is executed, the two variables to the right of the equal sign always stay the same, and it’s only the variable to the left that will be updated. In our case, we have a variable called result.

If that already holds a number prior to the calculation taking place, it would then be overridden with the new result of the calculation. Always put space in front and behind the arithmetic operators.

As your calculations become more complex you’ll start to use parenthesis and you must ensure that you insert blank characters before and after the parenthesis to separate them from your arithmetic operators.

One space is the minimum. You can, for instance, line up the code and make it a lot more readable. You can insert as many spaces as you want. It will all still work the same and this allows us to define our calculations across many lines within the ABAP editor.

Now as you can imagine, we’re not just stuck to calculating the value of variables. We can also use individual values in our calculation.

Arithmetic Subtraction

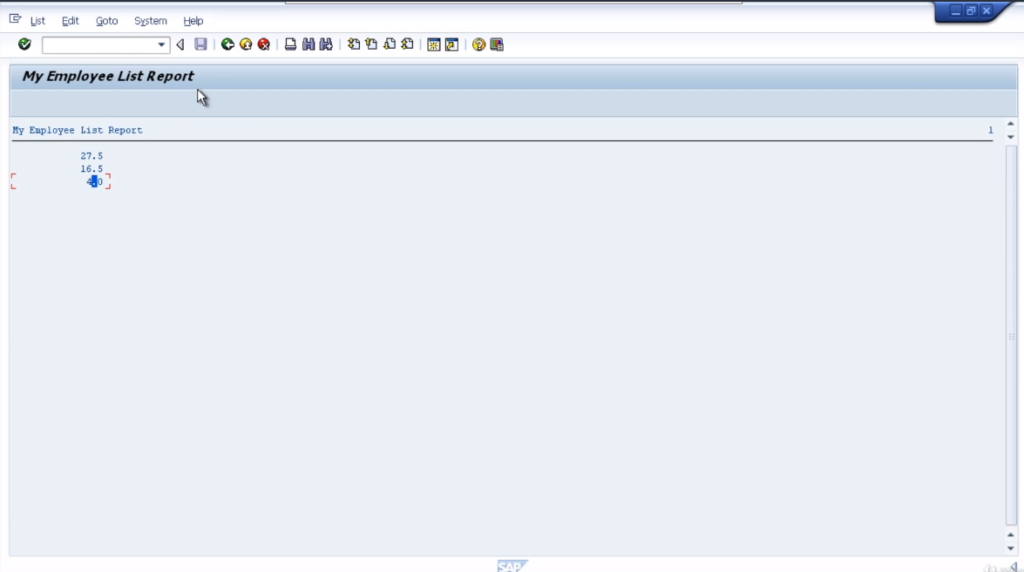
Let’s now have a very quick look at subtraction. Copy the previous example and change the plus sign to a minus sign. Take away minus 5.5 from 22. The result would be 22 minus, minus 5.5, and the result is 27.5. Now take away the minus sign. A quick test, 22 minus 5.5 is 16.5.

Result = integer01 – packed_decimal01

Write/result

Arithmetic Division

Now let’s have a look at division. Use / as a division sign. Replace the arithmetic sign in the previous example with a / sign and see the result. We get results as 4. Simple isn’t it!

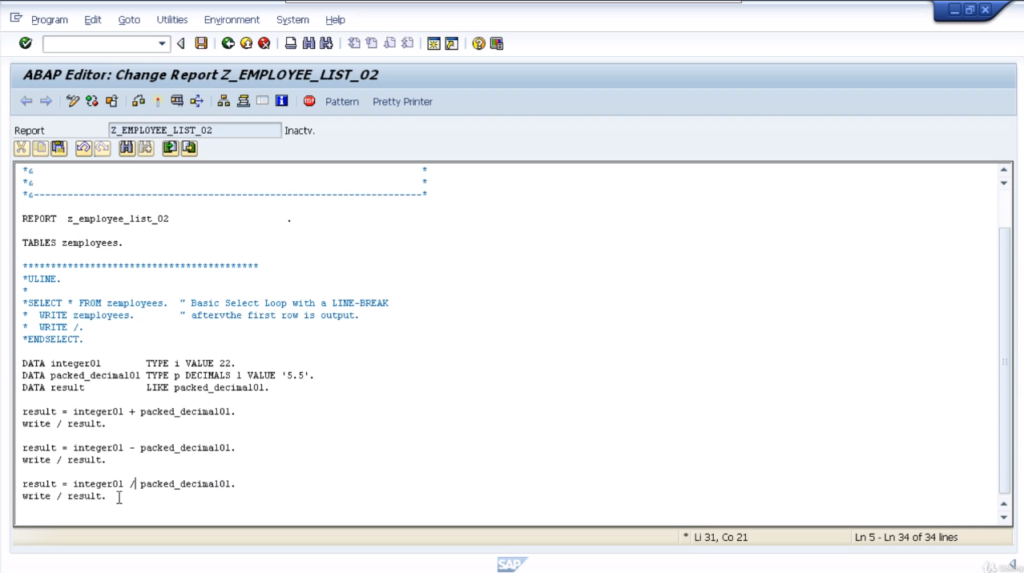
Result = integer01 / packed_decimal01

Write/result

Arithmetic Multiplication

The last arithmetic operation is multiplication. A very simple coding for it. Just change the sign in the previous example to the * sign. The result would be displayed.

Now just before we move on to the topic of conversion rules, you also have the option of using some other statements called ADD, SUBTRACT, DIVIDE, and MULTIPLY. Now the syntax for these is a little bit different. You can try them on your own too.

Result = integer01 * packed_decimal01

Write/result

Conversion Rules

As we’ve been creating this program, you’ll have no doubt seen we’re using various different data types when declaring our variables. Now, it’s a programmer’s responsibility to make sure the data types used are compatible with each other when you use them for calculations or moving data to and from those objects throughout your program.

You do not want to be performing any calculations on variables and numbers that do not match. For example, a variable defined as an integer cannot be multiplied by a character. The two data types are incompatible, and as a result, the system would generate syntax errors and a runtime error if you try to execute the program.

Now, SAP has built in some automatic data type conversions from many of the standard data types that are available within ABAP. There are scenarios where the inbuilt ABAP conversion rules are not appropriate and it is important that you become familiar with the inbuilt conversion rules, and know when to manipulate the data prior to using them in your calculations.

So, let’s take a look at the conversion rules that currently exist. Now you shall get an idea of what the conversion rules are and how you can use them throughout your programs. Now, conversion rules are predefined logic that determines how the contents of the source field can be entered into a target field.

If you have an integer field containing the value of one and try to insert that value into a character string, the built-in conversion rules will determine exactly how this should be done without throwing any syntax errors or runtime errors.

Let’s have a look at some examples. So, let’s suppose we add a variable called num1, a type packed decimal and we add the results. We add the result of the type integer. If we had a calculation where a packed decimal number was moved into an integer field, the inbuilt conversion rules would round the decimal places of num1, up or down, and insert the contents into the result one field.

So, let’s say we had a value of 3.33. So what we will get here is result one, with a result in a value of three. Probably best if we output this to our screen and check the result. We end up with a value of three.

That is so because the inbuilt conversion rules rounded the number down. If we add the value of 5.55, and this time, the result will contain the value 6 because the rounding will go up. Automatic conversion rules are applied.

As you work with different data types within your program, many different conversion rules will be applied automatically, and it’s up to you as the programmer to understand these conversion rules, understand the data types you are using within your program to ensure no run time errors will occur.

Division Variations

Now step back just a little bit and discuss the division operator. Earlier we saw the format of a simple division calculation. In ABAP, we have three different ways we can divide numbers together.

This allows us to concentrate on the remainder of the actual integer division, and the standard division result with decimal places. So let’s just go through these three so that you become familiar with them when you need to use them in your own program.

So back in the code. Let’s add another little separator. We’ll generate some division calculations. So here’s the first calculation. Just generate the outputs. Line them up for easiness to read.

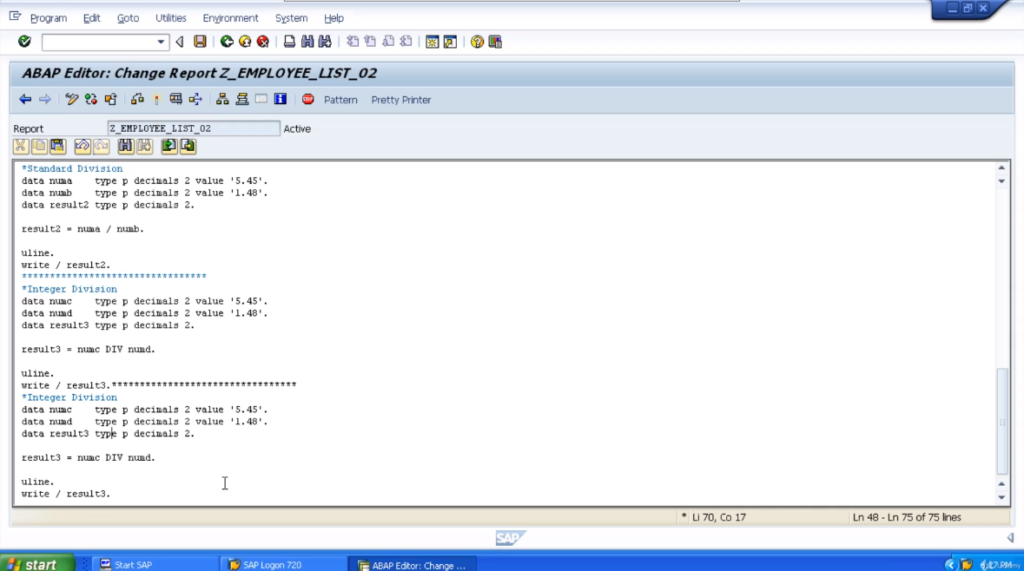
So we define three variables, numa, numb, and result2. Numa has two decimal places with a value of 5.45. Numb has two decimal places with a value of 1.48 and result2, which will be the product of our calculation.

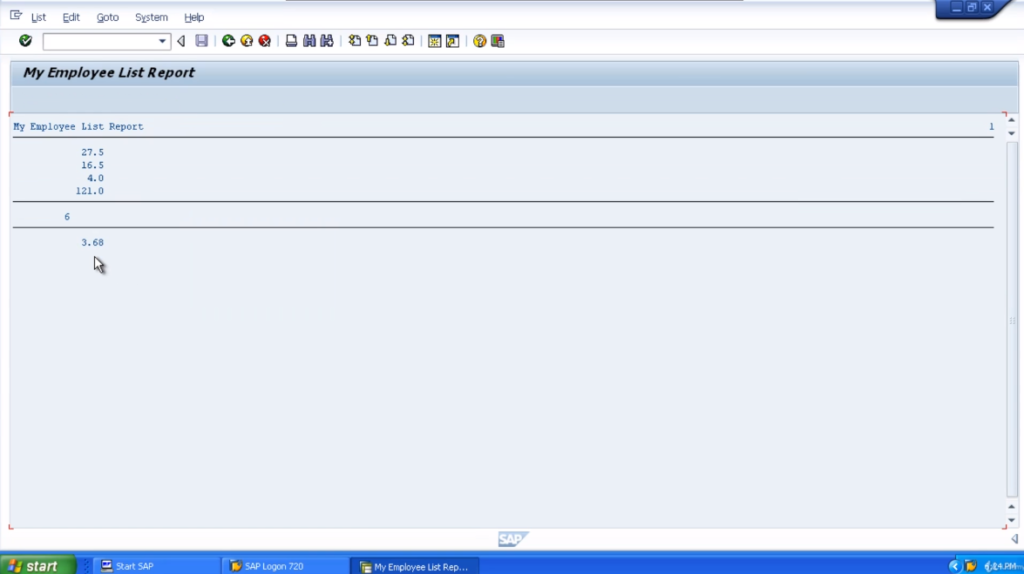
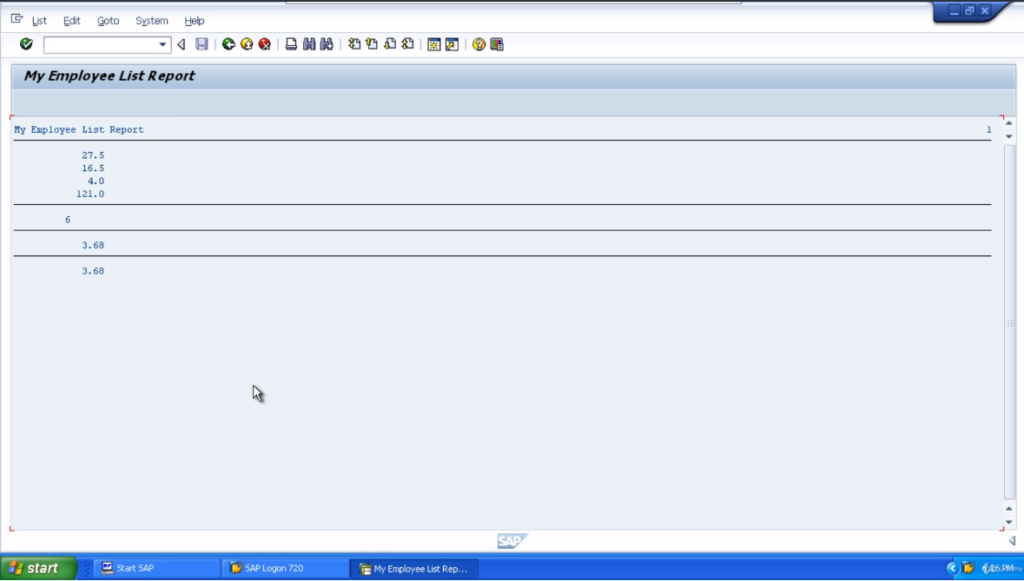
There we go. So our result will be numa divided by numb. Activate the program, and execute it. So the result is 3.68. So that’s the standard division. Nothing too spectacular there.

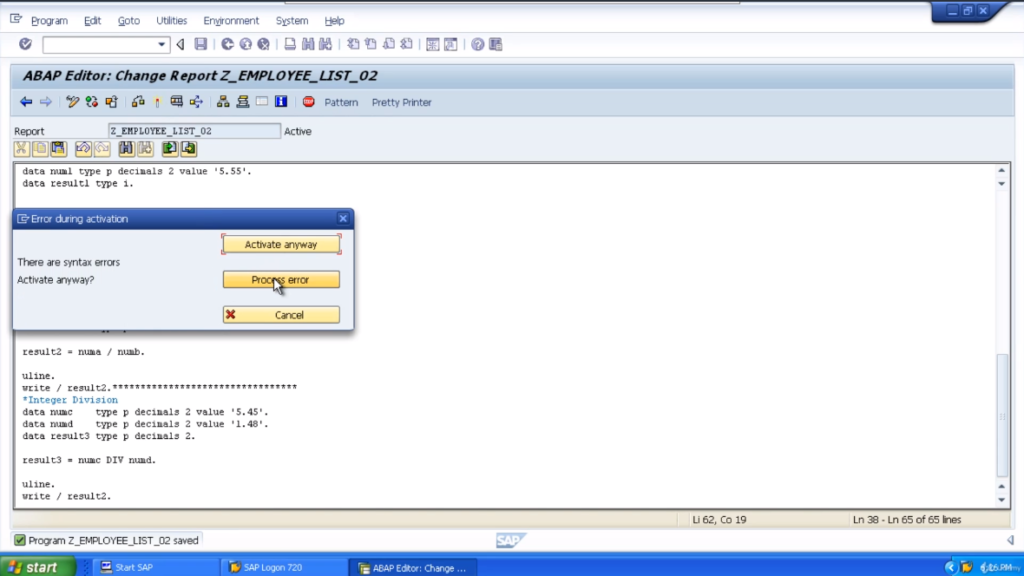
Now we’ll have a look at the integer division. So we’ll use the same values and obviously rename the actual variable names. Now for the integer division, instead of using the normal divide symbol, we actually use DIV.

So what’s integer division? Well as a reminder, what it will do, will divide one number by the other, but the result we’ll get is going to be the integer value. So this means we will not get the decimal places.

Let’s activate our program. Execute the program. We’re getting a result of 3. We’re just getting the integer, the full number, not the decimal places. So now, as you can probably guess, the last example we want to look at is the remainder.

Now with the remainder division type, we want to use MOD. So the result we get here is going to be the large number divided by the small, but we will only be shown the remainder value of what cannot be divided directly into numE. Let’s execute the program and see.

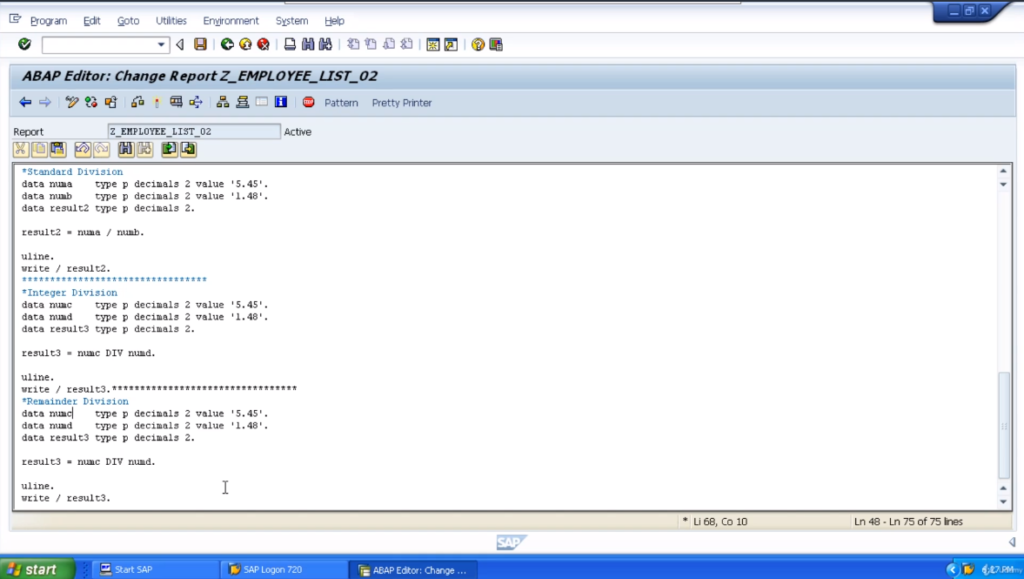
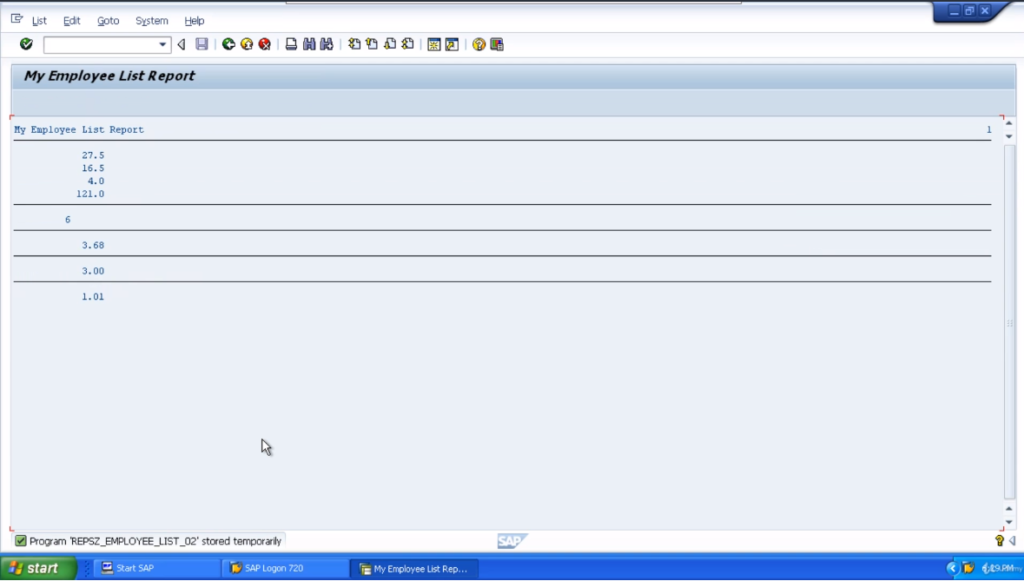
So now we’ve got a remainder of 1.01, which my calculations, should be correct. 5.45 divided by 3.48 3.6824. That means 3 times 1.48 gives us a value of 4.4. So if we take 4.4 from the 5.45, that gives us 1.01 which is the result we’ve got there.